1) Una compañía se abastece actualmente de cierto producto solicitando una cantidad suficiente para satisfacer la demanda de un mes. La demanda anual del artículo es de 1500 unidades. Se estima que cada vez que hace un pedido se incurre en un costo de $20. el costo de almacenamiento por inventario unitario por mes es de $2 y no se admite escasez.
a. Determinar la cantidad de pedido optima y el tiempo entre pedidos
b. Determinar la diferencia de costos de inventarios anuales entre la política óptima y la política actual, de solicitar un abastecimiento de un mes 12 veces al año.
Solución:
D= 1500 unidades/año
Cp =$20
Cmi =$2 unidad/mes x 12meses = $24 unidad/año
a)
b) Política Actual: se le agota cada mes o sea 1/12 año
Política optima:
Q*= 50
Diferencia
2) Una ferretería tiene que abastecer a sus clientes con 30 bolsas de cemento diarios siendo esta una demanda conocida. Si la ferretería falla en la entrega del producto pierde definitivamente el negocio, para que esto no suceda se asume que no existirá escasez. El costo de almacenamiento por unidad de tiempo es de $0.35 unidad al mes y el costo por hacer el pedido es de $55.
a) Cuál es la cantidad optima a pedir
b) El periodo de agotamiento (asumir 1 mes = 30 días, 1 año = 360 días)
Solución:
D = 30 bolsas / día = 900 bolsas / mes
Cmi= 0.35 unidad / mes
Cop= $55
a)
b)
3) FULL COURT PRESS, compra papel satinado en rollos de 1500 libras para imprimir libros de texto. La demanda anual es de 1920 rollos. El costo por rollos es de $ 1000 y el costo anual de manejo de inventarios es de 15% del costo. Cada pedido le cuesta $ 250.
a) ¿Cuántos rollos sería conveniente que pidiera de una sola vez FULL COURT PRESS?
b) ¿Cuál sería el tiempo entre pedidos?
Solución:
D = 1920 rollos
Cu = $ 1000
Cmi = 15% Cu
Cp = $250
a)
b)
4) Una compañía se abastece de un producto que se consume a razón de 50 unidades diarias. A la compañía le cuesta $25 cada vez que se hace un pedido y un inventario unitario mantenido en existencia por una semana costará $0.70. Determine el número óptimo de pedidos que tiene que hacer la compañía cada año, la cantidad por pedido y el tiempo del ciclo. Supóngase que la compañía tiene una política vigente de no admitir faltantes en la demanda y opera 240 días al año.
Solución:
Cmi = $ 0.70/ semana x 34 semanas/ año = $24/año
Cp = $ 25
D = 50 unid. / Día x 240 días = 12000 unidades
a)
b)
5) Un almacén vende 10,000 abanicos por año. Cada vez que se hace un pedido se incurre en un costo de $5. El almacén paga $100 por cada abanico, y el costo de mantener el inventario es de $1 durante un año, se estima como el costo de oportunidad anual de $20. Determine la cantidad óptima de pedido y el costo total.
Datos:
Cp.= $5
D= 10.000 abanicos/año
Cmi = $20/ año
Cu: $100 /abanico
a. Cantidad óptima de pedido
La cantidad que debe pedir el almacén es de 71 abanicos
b. Costo total
EOQ CON FALTANTES
1) Un agente de mercedes benz debe pagar 20 000 dólares por cada automóvil que compra, el costo anual de almacenamiento es de 25% del valor del automóvil, el agente vende 500 autos al año su costo por faltantes será de 20000 dólares. Cada vez que el agente coloca un pedido su costo es de 10 000 dólares determine:
a. La cantidad que debe ordenar el cada pedido Q
b. El máximo nivel de inventario.
c. el número de ordenes por año
d. El costo mínimo anual.
Solución
2) Una empresa vende un artículo que tiene una demanda de 18, 000 unidades por año, su costo de almacenamiento por unidad es de $ 1.20 por año y el costo de ordenar una compra es de $ 400.00. El costo unitario del artículo es $ 1.00. El costo por unidad de faltante es de $ 5.00 por año. Determinar:
a)La cantidad optima pedida
b)El costo total por año
Datos:
Cp.= $5
D= 10.000 abanicos/año
Cmi = $20/ año
Cu: $100 /abanico
a. Cantidad óptima de pedido
La cantidad que debe pedir el almacén es de 71 abanicos
b. Costo total
EOQ CON FALTANTES
1) Un agente de mercedes benz debe pagar 20 000 dólares por cada automóvil que compra, el costo anual de almacenamiento es de 25% del valor del automóvil, el agente vende 500 autos al año su costo por faltantes será de 20000 dólares. Cada vez que el agente coloca un pedido su costo es de 10 000 dólares determine:
a. La cantidad que debe ordenar el cada pedido Q
b. El máximo nivel de inventario.
c. el número de ordenes por año
d. El costo mínimo anual.
Solución
2) Una empresa vende un artículo que tiene una demanda de 18, 000 unidades por año, su costo de almacenamiento por unidad es de $ 1.20 por año y el costo de ordenar una compra es de $ 400.00. El costo unitario del artículo es $ 1.00. El costo por unidad de faltante es de $ 5.00 por año. Determinar:
a)La cantidad optima pedida
b)El costo total por año
c)El número de pedidos por año
d) El tiempo entre pedidos
Datos
C1= $ 1.00
C2 = $ 400.00
C3 = $ 1.20
C4 = $ 5.00
a) La cantidad óptima a pedir se calcula de la siguiente forma.
=3465unidades
b) El costo total estará determinado por:
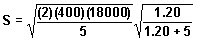=747 unidades
Datos
C1= $ 1.00
C2 = $ 400.00
C3 = $ 1.20
C4 = $ 5.00
a) La cantidad óptima a pedir se calcula de la siguiente forma.
=3465unidadesb) El costo total estará determinado por:
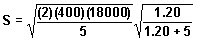=747 unidades
c) el numero de pedidos por año es
=4.66d) El tiempo entre pedidos es
=0.2153. La demanda de un artículo es de 1.000 unidades al mes, se permite déficit. Si el costo unitario es de $1,50, el costo de hacer una compra es de $600, el costo de tenencia de una unidad es de $2 por año y el costo de déficit es de $10 por unidad al año, determinar:
a. La cantidad optima que debe comprarse
b. El número óptimo de unidades agotadas (déficit)
Solución:
D= 1000 unidades/mes = 12.000 unidades/año
Cmi = 2 $/unidad
Cp= 600 $/unidad
Cu= $1,50
Cf = 10 $/unidad
Solución
a
b
4) Un agente de mercedes benz debe pagar 20 000 dólares por cada automóvil que compra, el costo anual de almacenamiento es de 25% del valor del automóvil, el agente vende 500 autos al año su costo por faltantes será de 20000 dólares. Cada vez que el agente coloca un pedido su costo es de 10 000 dólares determine:
a) La cantidad que debe ordenar.
b) El máximo nivel de inventario.
c) el número de órdenes por año.
Datos:
Cp. = 10000 dólares /orden
D= 500 autos/año
Cmi = (0.25) (20000) = 5000 dólares /auto /año
Cf= 20000 dólares/unidad/año
a. La cantidad que debe ordenar.
b. El máximo nivel de inventario.
c. el número de órdenes por año.
LEP SIN FALTANTES
1. Una compañía tiene una variada línea de productos. Uno de ellos es la pintura de látex. La compañía puede fabricar pintura a una tasa anual de 8000 galones. El costo unitario de producir un galón de pintura es $0.31 y el costo anual de mantener el inventario es 40%. Antes de cada corrida de producción se realiza la limpieza y verificación de las operaciones a un costo de $30. Determine la cantidad económica a producir y el costo total del inventario promedio anual.
Solución.
Cop = $30 por preparación
Cmi = 40% anual
Cu= $0.31 por galón
Cmi x Cu = 0.40 x $0.31 = $0.124 por galón por año
D = 4000 galones por año
R = 8000 galones por año
a)
b) Costo total anual
2 Uno de los artículos que produce Mattel es una muñeca barbie. Tiene una demanda constante de 40000 piezas por año. El cuerpo de plástico suave es el mismo para todas las muñecas, pero la ropa se cambia periódicamente para ajustarse a los diferentes gustos. La empresa puede fabricar 200 artículos por día, pero solo trabaja 200 días al año. Las corridas de producción para diferentes productos requieren los cambios para las cortadoras y las máquinas de coser, y algunos ajustes en el área de ensamble. La preparación se estima en $350 por corrida de producción. Una muñeca que se vende por $15000 cuando sale de la línea de producción. Los costos completos de acarreo para los artículos de la producción se establecen en 20% del costo de producción y se basan en el nivel promedio del inventario. A partir de estas cifras para el costo, calcule la cantidad económica de producción y el nivel máximo de inventario.
Solución
C op = $350 por preparación
Cmi = 20% anual
Cu= $15000 por muñeca
Cmi x Cu = 0.20 x $15000 = $3000 muñecas por año
D= 40000 muñecas por año
R = 200 x 200 = 400000 muñecas al año
3. Un gran productor de medicina para los nervios produce sus provisiones en remesas, el costo de preparación para cada remese es de $750. De la producción se obtiene 48 galones diarios del producto y cuesta $0.05 cada uno para conservarlos en existencia. La demanda constante es de 600 galones al mes. Suponga 12 meses, 300 días al año y 25 días al mes. Encuentre la cantidad óptima de producción, el tiempo de ciclo óptimo, la existencia máxima en inventario y la duración en días de cada mes de producción
Solución:
Cop= $750
Cmi= $0.05 /mes
R = 48 gal/día x 25 días = 1,200 galones / mes
D = 600 gal /mes
4. Un contratista debe suministrar 10.000 cojinetes diarios a un fabricante de automóviles. El encuentra que cuando empieza el lote de producción puede producir 25.000 cojinetes al día. El costo de mantener un cojinete en inventario al año es de $ 2 y el costo de alistar cada lote de producción es de $ 1.800.
a) ¿Qué tamaño del lote debe producirse?
b) ¿Qué tan frecuente deben producirse los lotes para satisfacer la demanda (en días) si se consideran 250 días al año?
c) ¿Cuánto tiempo durará su ciclo de producción?
LEP SIN FALTANTES
1. Una compañía tiene una variada línea de productos. Uno de ellos es la pintura de látex. La compañía puede fabricar pintura a una tasa anual de 8000 galones. El costo unitario de producir un galón de pintura es $0.31 y el costo anual de mantener el inventario es 40%. Antes de cada corrida de producción se realiza la limpieza y verificación de las operaciones a un costo de $30. Determine la cantidad económica a producir y el costo total del inventario promedio anual.
Solución.
Cop = $30 por preparación
Cmi = 40% anual
Cu= $0.31 por galón
Cmi x Cu = 0.40 x $0.31 = $0.124 por galón por año
D = 4000 galones por año
R = 8000 galones por año
a)
b) Costo total anual
2 Uno de los artículos que produce Mattel es una muñeca barbie. Tiene una demanda constante de 40000 piezas por año. El cuerpo de plástico suave es el mismo para todas las muñecas, pero la ropa se cambia periódicamente para ajustarse a los diferentes gustos. La empresa puede fabricar 200 artículos por día, pero solo trabaja 200 días al año. Las corridas de producción para diferentes productos requieren los cambios para las cortadoras y las máquinas de coser, y algunos ajustes en el área de ensamble. La preparación se estima en $350 por corrida de producción. Una muñeca que se vende por $15000 cuando sale de la línea de producción. Los costos completos de acarreo para los artículos de la producción se establecen en 20% del costo de producción y se basan en el nivel promedio del inventario. A partir de estas cifras para el costo, calcule la cantidad económica de producción y el nivel máximo de inventario.
Solución
C op = $350 por preparación
Cmi = 20% anual
Cu= $15000 por muñeca
Cmi x Cu = 0.20 x $15000 = $3000 muñecas por año
D= 40000 muñecas por año
R = 200 x 200 = 400000 muñecas al año
3. Un gran productor de medicina para los nervios produce sus provisiones en remesas, el costo de preparación para cada remese es de $750. De la producción se obtiene 48 galones diarios del producto y cuesta $0.05 cada uno para conservarlos en existencia. La demanda constante es de 600 galones al mes. Suponga 12 meses, 300 días al año y 25 días al mes. Encuentre la cantidad óptima de producción, el tiempo de ciclo óptimo, la existencia máxima en inventario y la duración en días de cada mes de producción
Solución:
Cop= $750
Cmi= $0.05 /mes
R = 48 gal/día x 25 días = 1,200 galones / mes
D = 600 gal /mes
4. Un contratista debe suministrar 10.000 cojinetes diarios a un fabricante de automóviles. El encuentra que cuando empieza el lote de producción puede producir 25.000 cojinetes al día. El costo de mantener un cojinete en inventario al año es de $ 2 y el costo de alistar cada lote de producción es de $ 1.800.
a) ¿Qué tamaño del lote debe producirse?
b) ¿Qué tan frecuente deben producirse los lotes para satisfacer la demanda (en días) si se consideran 250 días al año?
c) ¿Cuánto tiempo durará su ciclo de producción?
Solución
Cop = $1800
Cmi= $2/año
R = 25000 unid. /día
D = 10000 cojines
5. La demanda de una empresa para un artículo es de 18.000 unidades al año. El costo de organizar o preparar la orden de producción es de $500 y el costo de almacenamiento de una unidad por año es de $1.8.
a) Cuál debe ser la cantidad óptima del lote que debe manufacturar y el costo total (almacenamiento y preparación); si la tasa de producción diaria es de 100 unidades y la demanda de 72 unidades por día.
b) Calcular el nivel de inventario máximo.
c) Estimar el tiempo de producción.
Solución
D = 72 unidades / día
Cop = $ 500
Cmi = $1.8
R = 100 unidades/ día
a)
b)
c)
LEP CON FALTANTES.
1. Súper Sauce produce un aderezo de ensalada. La demanda de este aderezo es alrededor de 400 libras por mes y Súper Sauce puede fabricar a una tasa de 2000 libras por mes. Para iniciar la producción, tiene que verificar y limpiar las maquinas en forma exhaustiva y cada preparación cuesta $ 120. El costo de producir este aderezo es $3 por libra y el costo de mantenerlo en inventario se estima en 20% anual. Si la demanda de este aderezo excede a lo disponible en inventario la orden se surte después. La administración piensa que los faltantes incurren en dos tipos de costo, la perdida de buena voluntad y una sanción por el faltante. La pérdida de la buena voluntad se estima en $ 0.1 por libra y la sanción se estima en $ 1.2 por libra que falta por mes. Analice este problema.
LEP CON FALTANTES.
1. Súper Sauce produce un aderezo de ensalada. La demanda de este aderezo es alrededor de 400 libras por mes y Súper Sauce puede fabricar a una tasa de 2000 libras por mes. Para iniciar la producción, tiene que verificar y limpiar las maquinas en forma exhaustiva y cada preparación cuesta $ 120. El costo de producir este aderezo es $3 por libra y el costo de mantenerlo en inventario se estima en 20% anual. Si la demanda de este aderezo excede a lo disponible en inventario la orden se surte después. La administración piensa que los faltantes incurren en dos tipos de costo, la perdida de buena voluntad y una sanción por el faltante. La pérdida de la buena voluntad se estima en $ 0.1 por libra y la sanción se estima en $ 1.2 por libra que falta por mes. Analice este problema.
Solución: Los parámetros del problema son
Cop = $120 por preparación
Cmi = 20% anual
c = $3 por libra
h = 0.2 x $3 = $0.6 por libra por año
p = $0.1 por libra
= $1.2 por libra por mes = $14.4 por libra por año
D = 400/mes =4800/año
R = 2000/mes = 24000/año
la cantidad económica a producir es
El máximo nivel de faltante óptimo es:
El tamaño del lote económico es 1605 libras, el máximo nivel de ordenes atrasadas es 26 libras y la producción toma 4800/24000 0 20% del tiempo. El costo total del inventario es:
Cop = $120 por preparación
Cmi = 20% anual
c = $3 por libra
h = 0.2 x $3 = $0.6 por libra por año
p = $0.1 por libra
= $1.2 por libra por mes = $14.4 por libra por año D = 400/mes =4800/año
R = 2000/mes = 24000/año
la cantidad económica a producir es
El máximo nivel de faltante óptimo es:
El tamaño del lote económico es 1605 libras, el máximo nivel de ordenes atrasadas es 26 libras y la producción toma 4800/24000 0 20% del tiempo. El costo total del inventario es:
2. Cada año la Samltown Optometry Clinic Vende 10,000 armazones para lentes la clínica pide las armazones a un abastecedor regional, que cobre 14 dólares por armazón. Cada pedido incurre en un costo de 50 dólares. La óptica cree que se demanda de armazones puede acumularse y que el costo por carecer de un armazón durante un año es 15 dólares debido a la pérdida de negocios futuros. El costo anual por mantener un inventario es de 30 centavos por dólar del valor del inventario. ¿Cuál es la cantidad óptima de pedido? ¿Cuál es la escasez máxima que se presentará? ¿Cuál es el nivel máximo de inventario que se presentará?
Solución:
Precio del inventario = $15 por armazón
C3=$50 por pedido
C2=$15 unidad/año
C1=$0.30 por dólar del valor del inventario
el costo 1 corresponde
C1=0.30 * valor del inventario = 0.30(15) = $4.50
C1=$4.50
Solución:
Precio del inventario = $15 por armazón
C3=$50 por pedido
C2=$15 unidad/año
C1=$0.30 por dólar del valor del inventario
el costo 1 corresponde
C1=0.30 * valor del inventario = 0.30(15) = $4.50
C1=$4.50
r=10,000 armazones al año.
Para Q* (cantidad optima de pedido)
¿Cuál es el nivel máximo de inventario?
¿Cuál es la escasez máxima que se presentara?
Carencia máxima = Q* - S* = 573.48 – 413.45 = 124.03 armazones
O bien
3. La demanda de un articulo de una determinada compañía es de 18, 000 unidades por año y la compañía puede producir ese articulo a una tasa de 3 000 unidades por mes, El costo de organizar una tanda de producción es $ 500.00 y el costo de almacenamiento de una unidad es de $ 0.15 por mes. Determinar la cantidad optima de debe de manufacturarse y el costo total por año suponiendo que el costo de una unidad es de $ 2.00. El costo por unidad agotada es de $ 20.00 por año.
Datos
D = 18, 000 Unidades por año
R = 3,000 por mes
C1 = $ 2.00
C2 = $ 500.00
C3 = $ 0.15 por mes
C4 = $ 20.00 por año
La cantidad optima estará definida por:
Para Q* (cantidad optima de pedido)
¿Cuál es el nivel máximo de inventario?
¿Cuál es la escasez máxima que se presentara?
Carencia máxima = Q* - S* = 573.48 – 413.45 = 124.03 armazones
O bien
3. La demanda de un articulo de una determinada compañía es de 18, 000 unidades por año y la compañía puede producir ese articulo a una tasa de 3 000 unidades por mes, El costo de organizar una tanda de producción es $ 500.00 y el costo de almacenamiento de una unidad es de $ 0.15 por mes. Determinar la cantidad optima de debe de manufacturarse y el costo total por año suponiendo que el costo de una unidad es de $ 2.00. El costo por unidad agotada es de $ 20.00 por año.
Datos
D = 18, 000 Unidades por año
R = 3,000 por mes
C1 = $ 2.00
C2 = $ 500.00
C3 = $ 0.15 por mes
C4 = $ 20.00 por año
La cantidad optima estará definida por:
Para calcular el costo anual primero se deben calcular el numero de unidades agotadas.
El costo total quedara definido por
Costo Total = $ 39, 855 por periodo de planeacion.
4. En una empresa fabricadora de juguetes ,cada vez que se produce un lote se incurre en un costo de preparación $30, El costo de mantenimiento de inventario de un juguete es de $0.5 mes, la demanda es 15.000 juguetes anuales y la tasa anual es de 20.000 juguetes.Cada juguete que falta cuando se necesita cuesta $20.Indique cual es la cantidad optima a pedir.
5. la demanda de un articulo en una empresa es de 36000 unidades al año y la empresa puede producir este articulo a una tasa de 6000 unidades por mes. El costo de organizar una corrida de producción es de $1000 y el costo de almacenamiento de una unidad al mes es de $30 centavos, el costo de una unidad es de $4 y el costo de una unidad agotada es de $40 por año. Se pide calcular la cantidad óptima pedida, la cantidad agotada y el inventario máximo
Datos:
Demanda= 36000
Costo de una corrida de producción = $1000
Costo de almacenamiento= $0.30
Costo de una unidad = $4
Costo de una unidad agotada = $40
Tasa de producción = 6000
La cantidad optima
b cantidad agotada
c inventario máximo
REFERENCIA
Métodos cuantitativos para los negocios, Anderson, Sweeney, Williams, novena edición
Grace Acosta Villalobos
El costo total quedara definido por
Costo Total = $ 39, 855 por periodo de planeacion.
4. En una empresa fabricadora de juguetes ,cada vez que se produce un lote se incurre en un costo de preparación $30, El costo de mantenimiento de inventario de un juguete es de $0.5 mes, la demanda es 15.000 juguetes anuales y la tasa anual es de 20.000 juguetes.Cada juguete que falta cuando se necesita cuesta $20.Indique cual es la cantidad optima a pedir.
5. la demanda de un articulo en una empresa es de 36000 unidades al año y la empresa puede producir este articulo a una tasa de 6000 unidades por mes. El costo de organizar una corrida de producción es de $1000 y el costo de almacenamiento de una unidad al mes es de $30 centavos, el costo de una unidad es de $4 y el costo de una unidad agotada es de $40 por año. Se pide calcular la cantidad óptima pedida, la cantidad agotada y el inventario máximo
Datos:
Demanda= 36000
Costo de una corrida de producción = $1000
Costo de almacenamiento= $0.30
Costo de una unidad = $4
Costo de una unidad agotada = $40
Tasa de producción = 6000
La cantidad optima
b cantidad agotada
c inventario máximo
REFERENCIA
Métodos cuantitativos para los negocios, Anderson, Sweeney, Williams, novena edición
Grace Acosta Villalobos
